イアン・スチュアート 著 徳田 功 訳 「不確実性を飼いならす」メモ
イアン・スチュアート著 徳田 功訳
「不確実性を飼いならす 予測不能な世界を読み解く科学」メモ
5 情報が多すぎる
----------------------------------------------------------------------------------
【まとめ】
・最小二乗法:誤差の二乗の総和を最小にすることで、最小の誤差を求めることができる。
・中心極限定理:試行回数が多い場合に二項分布は正規分布に近き、同じ確率分布から抽出されたどんな確率変数の標本の総和も、正規分布に近づく
・正規分布を用い、計測結果がある特定の範囲に含まれる確率を計算可能。
----------------------------------------------------------------------------------
・統計学:確率論の応用分野
・統計学は天文学と社会学という異なる分野から生まれた。
・二つの分野の共通点:不完全なデータから有益な情報を抽出すること。
★天文学と多すぎるデータ
・天文学の問題:数理モデルと観測結果の比較
すべての観測結果には制御不能な誤差が含まれている・代数方程式の解と誤差解析→データが多すぎると誤った方法に導く
・代数学の最悪の特性:未知変数よりも多くの方程式があると、原則として解が存在しない。(優決定系)
・微分方程式による誤差解析:誤差を含む数を複数組み合わせると、結果に含まれる誤差はもっと大きくなる。
★オイラー、多すぎるデータに挑む
・8つの未知数を含む75個の方程式の解を求める。
→オイラーは2個の解を先に求めたが、さらに優決定性が強まり、解を求めることができなかった。
・天文学者マイヤー:月のクレーター観測を行い、3つの未知数を含む方程式27個を得た。
・全データを3つのグループに分け、各グループで9個の方程式を足し合わせ、1個の式にした。
→3つの未知数を含む3個の方程式を得た(通常の方法で解ける)
・似ているように見える式を選んでグループ分けすることで、「数値不安定性」を避けた。
・最悪の状況:個々の誤差がすべて組み合わさり、誤差の総和が最大になる状況を重視
・望ましい状況:もっとも確からしい全体の誤差
★ルジャンドルと最小二乗法
・ルジャンドルの定式化:線形方程式の優決定系が与えられたとき、これらの式を満たす未知数のうち、全体の誤差を最小にするものはどれか。
・誤差を完全に取り除くことは不可能
→重要なのは、誤差をどれだけゼロに近づけられるか
・全体の誤差の定義
・すべての誤差を正の数に変換(二乗)して足し合わせる。
・誤差の二乗の総和を最小にすることで、最小の誤差を求めることができる。
・「不確実性にどう対処するか?」
ルジャンドルの答え:「不確実性をできる限り小さくせよ」
・任意のデータの集まりに対し、最小二乗法で求められる最適な推定値は、データの平均。
★ド・モアブルと正規分布
・二項係数は数が大きくなると計算困難。
→二項分布を近似する必要あり
・ド・モアブルは分布の中心に位置する最も大きな二項係数の近似値を求めた。2^(n+1)/√(2πn) (n:試行回数)
・他の二項係数の値も推定し、ベルヌーイの二項分布を「正規分布」に関係づけた。
<正規分布>
・二項分布のような曲線を形成し、真ん中に頂点が一つだけある。
・頂点を中心に左右対称、中央から離れると急速に減少する。
・この曲線で作られる総面積は有限、その面積は1。
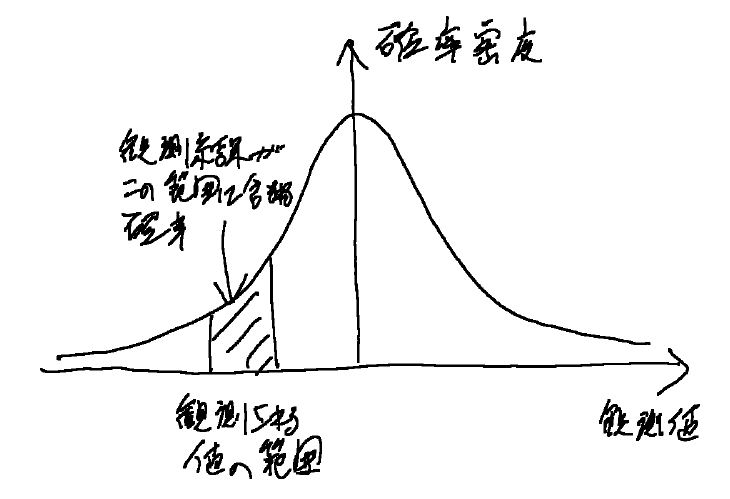
・正規分布は特定の値が観測される確率を与えるものではない。
・観測結果が与えられた値の範囲内に含まれる確率を与える。
・この確率は、その範囲の曲線の下の部分の面積に相当する。
・平均と標準偏差に関わるパラメータを用いて軸の「尺度」を変える。
・このような曲線の定式化は次式で与えられる。1/√(2πσ^2)*e^(-(x-μ)^2/2σ^2)
μ:平均(曲線の中央にある頂点の位置に対応)
σ:標準偏差(曲線の広がり、頂点周りの領域がどの程度広いかを測る)
・平均:正規分布に従うデータの平均化された値を意味する。
・標準偏差:平均を中心に値がどの程度散らばっているかを示す。
・分散:標準偏差の二乗σ^2
・面積は1に等しい。
・ド・モアブルの大発見:試行回数nが大きくなると、二項分布の棒グラフが正規分布と同じ形になる。
★ラプラスと中心極限定理
<中心極限定理>
・試行回数が多い場合に二項分布は正規分布に近づくことを証明。
・同じ確率分布から抽出されたどんな確率変数の標本の総和も、正規分布に近づく。
・この定理により、正規分布は統計学および確率論で特別な役割を果たすようになった。
・個々の観測値は、誤差のため、ある範囲の中で変動する。
・観測に伴う「誤差の分布」がわかれば、ある大きさの誤差がどれくらい起こりやすいかがわかる。
・中心極限定理より、観測を何度も繰り返し、その平均をとれば、誤差分布は問題にならない。
・観測を繰り返し行うと、観測の平均を得る。
・結果としてたくさんの平均が得られ、この平均自体も固有の確率分布に従う。
・この分布が正規分布に近づき、十分な回数の観測を組み合わせれば、よりいっそう正規分布に近くなる。
・未知の誤差分布:正規分布の平均と標準偏差に影響を与えるが、全体の形状には影響しない。
・正規分布の平均:誤差分布の平均と同じ値になる。
・正規分布の標準偏差:誤差分布の標準偏差を観測回数の平方根で割ったもの。
・観測回数が大きくなる→平均された観測地は平均値のまわりに密集する。
・観測誤差が多数の小さな誤差の組み合わせの結果であれば、誤差曲線は(近似的に)正規分布に従うはず、と中心極限定理は示唆する。
・中心極限定理は、最小二乗法(による平均化の操作)が、標準的な確率論の枠組みにおいて、最良の推定であることを示唆。
<サイコロ振りの総和>
1個のサイコロ
真ん中は3と4の間→3.5
2個のサイコロ
真ん中は6と8の間→7
観測の平均→7/2 = 3.5
3個のサイコロ
真ん中は10と11の間→10.5
観測の平均→10.5/3 = 3.5・ある与えられた分布から観測された値の平均をとると、その分布の元々の平均と同じ値を得る。
・標準偏差は、1個、2個、3個のサイコロについて1.71、1.21、0.99となる。(標準偏差 s=√((観測値-平均値)^2)/総数))
・中心極限定理より、これらの比率は1 対 1/SART(2) 対 1/SQRT(3)。
★正規分布と事象の起こりにくさ
・正規分布を用い、計測結果がある特定の範囲に含まれる確率を計算可能。
・観測値が平均からある特定の幅だけ隔たっている確率は、対応する正規分布曲線の下の部分の面積を計算して求められる。
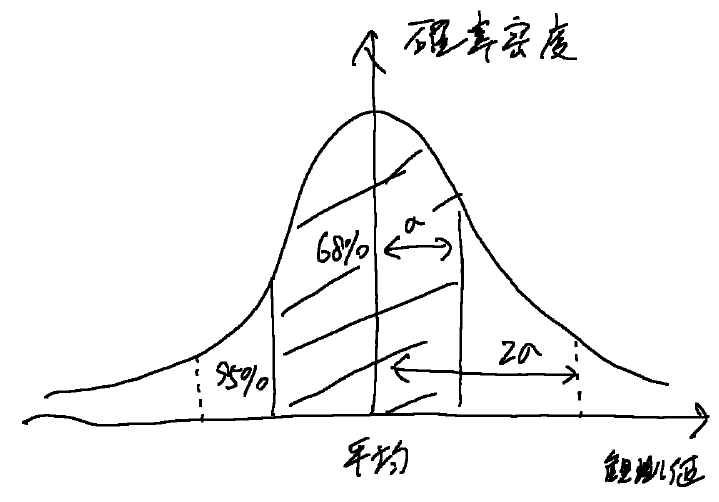
・正規分布の横軸は標準偏差σで縮尺可能。
・標準偏差σを単位にして、知りたい範囲の幅を測る。
・平均との差が大きくなるほど、確率はより急速に減少。
・平均との差が σよりも大きくなる確率 31.7%
2σ 4.5%
3σ 2.6%
4σ 0.006%
5σ 0.00006%
6σ 0.0000002%
★確率とは何か?
<確率論の現実への応用>
・確率がある特定の形で現実に関わっているという仮説をたてる
・公理を用いて仮説の結果を計算、実験結果と比較、仮説を検証。
・確率を表す面積の一般化には、確率を「測度」に対応させる必要がある。
・測度:面積のようなものを、事象空間の適切な部分集合(可測集合)に割り当てたもの
・標本空間:事象と呼ばれる部分集合を集めたものと、事象に対する測度Pからなる。
・Pは測度であり、全体集合の測度は1
・これ以外に必要なのは、事象の集まりが集合論的性質を満たし、測度は台(測度の値が0にならない点からなる集合)を持つという条件。
・ある集団における男子と女子の比を比べるとき、実際の標本空間は、その集団に含まれるすべての子供たち。
・四つの事象(空集合0、女子G、男子B,全体集合{G,B})からなる確率空間を比較
・男子の確率と女子の確率が等しいならば確率は次式となるP(0)=0、P(G)=P(B)=1/2、P({G,B})= 1